Las más importantes curvas que se usan actualmente en el diseño computacional son las curvas de Bézier y los B-Splines. Es gracias al trabajo de dos matemáticos franceses, Bézier y de Casteljau, que se desarrollan aplicaciones para el incipiente diseño computacional de los años 60, bajo el alero de la industria automotriz.
El resultado son herramientas que los diseñadores ocupan regularmente, bajo el nombre genérico de «trazados» o diseño vectorial, cuya matemática opera tras bambalinas con las ideas que estos matemáticos franceses, y otros más, desarrollaron.
Esta entrada participa en el Noveno carnaval de matematicas en español, organizado en el Blog Rescoldos en la trébede.
Esta entrada participa en el Noveno carnaval de matematicas en español, organizado en el Blog Rescoldos en la trébede.
A fines de los cincuenta Pierre Bézier y Paul de Casteljau se dedicaban esencialmente a los mismos problemas, ambos en la industria automotora (Renault y Citroen, respectivamente), y como ha sucedido en otras ocasiones, llegan esencialmente al mismo tipo de curvas, aunque con recursos matemáticos distintos.
El problema general surge ante la necesidad trazar curvas con mucha precisión, para lograr distintas piezas que puedan ensamblar correctamente.
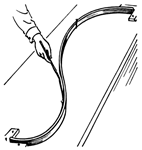
Para ello, los diseñadores de la época solían ocupar procedimientos de dibujo, por ejemplo, para trazar una aproximación de una curva que une dos puntos, usando las llamadas reglas francesas, o bien curvaban listones para generar lo que ahora se denomina «spline» (astilla, en inglés).
Pero de tal forma, no siempre se lograba la precisión necesaria; aunque ambos métodos ahora tienen su equivalente computacional, respectivamente, las Curvas de Bézier y las Splines, ambos elementos fundantes del diseño vectorial.
Bézier y de Casteljau

Curva de Bézier en un Cubo
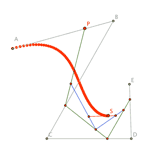
La primera versión de las curvas de Bézier fue en realidad tridimensional, un esquema basado en curvas cuadráticas construidas dentro de un cubo, método que le permitirá describir cualquier curva de grado 2 a partir de sólo cuatro puntos.
El método parte por describir una curva usando usando ecuaciones paramétricas de la forma y = x2. Luego, al transformar el cubo en un paralelepípedo cualquiera, la curva se transformará también. Así, los puntos de control son los vértices de un paralelepípedo imaginario.
Con el tiempo este esquema se simplificará más, de manera que pueda describir curvas cuadráticas a partir de sólo tres puntos, y como veremos más adelante, curvas de grado n con sólo n+1 puntos.
Unos años antes que Bézier, de Casteljau trabaja en esencialmente la misma idea, pero desde una perspectiva numérica. El ahora conocido como algoritmo de de Casteljau, es un método de aproximación numérica de los llamados polinomios de Bernstein, con los que se construye la ecuación de las curvas de Bézier:
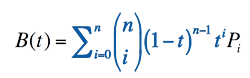
La porción en azul de la ecuación corresponde a un polinomio de Bernstein de grado «n», y el resto corresponde a los puntos de control de la curva de Bézier.
No hay comentarios.:
Publicar un comentario