Circunferencia

         TEORÍA DE LA                     CIRCUNFERENCIA

Hemos obtenido a partir de la ecuación ordinaria, la ecuación general de una circunferencia.

Pero dada una ecuación que tiene este aspecto:

$$x^2+y^2+Dx+Ey+F=0$$

Si se la pasa a la forma de ecuación ordinaria: ¿siempre se obtendrá una circunferencia?

Para responder esto vamos a recordar cómo se completa cuadrados con un ejemplo.

Ejemplo

Vamos a completar cuadrados en la siguiente expresión:
$$x^2+y^2–4x+2y–1=0\left[1\right]$$

La pregunta es: ¿qué lugar geométrico representa esta ecuación? ¿Estamos seguros de que es una circunferencia? Tendremos que llevarla a la forma ordinaria.

La idea es transformar:

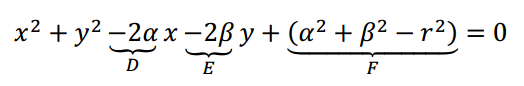
Y además:

Empecemos con $x^2–4x$

¿Qué le falta a esta expresión para ser un trinomio cuadrado perfecto? Falta el término independiente. Sabemos que el término independiente deberá ser la mitad de 4, elevado al cuadrado.

Entonces podemos sumar y restar $2^2$:

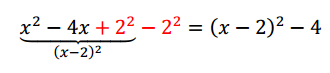
Ahora con la expresión para la variable $y$:

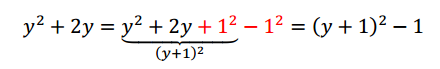
Reemplazamos en la $\left[1\right]$:

$${\left(x–2\right)}^2–4+{\left(y+1\right)}^2–1–1=0$$

Y ahora reordenamos para obtener la ecuación de la circunferencia:

$${\left(x–2\right)}^2+{\left(y+1\right)}^2=6$$

¿Cuáles son el centro y el radio?

$$C=\left(2,–1\right)$$

$$r=\sqrt{6}$$