Elipse

Elipse

Definición y ecuación canónica de la elipse

Dados dos puntos F1F1 y F2F2 llamados focos, se denomina elipse al conjunto de puntos del plano tales que la suma de sus distancias a ambos focos es constante:

E={P(x,y)|d(P,F1)+d(P,F2)=cte}E={P(x,y)|d(P,F1)+d(P,F2)=cte}

A esa constante la llamamos 2a2a.

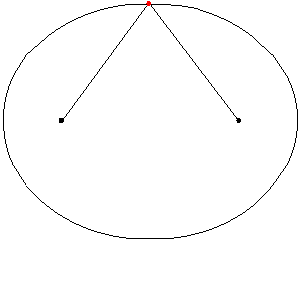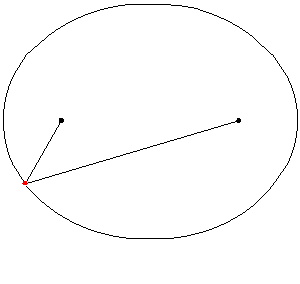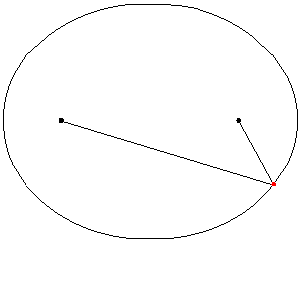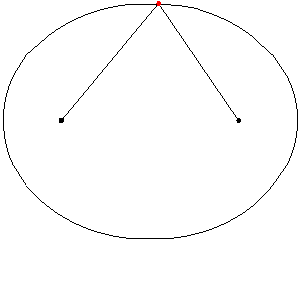
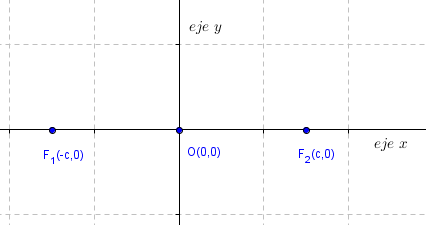
Consideremos que los focos son los puntos de coordenadas F1(–c,0)F1(–c,0) y F2(c,0)F2(c,0) con c>0c>0, y el punto medio entre los focos, se denomina centro C(0,0)C(0,0). En el siguiente esquema se pueden visualizar estos elementos:

Si la distancia entre los focos es d(F1,F2)=2cd(F1,F2)=2c , la condición para que sea una elipse es:

a>c>0a>c>0

Si elevamos al cuadrado:

a2>c2a2>c2

A la diferencia se la llama b2b2:

a2–c2=b2a2–c2=b2

⇒a2=b2+c2⇒a2=b2+c2

Haciendo una deducción se llega a:

x2a2+y2b2=1,a>b>0x2a2+y2b2=1,a>b>0

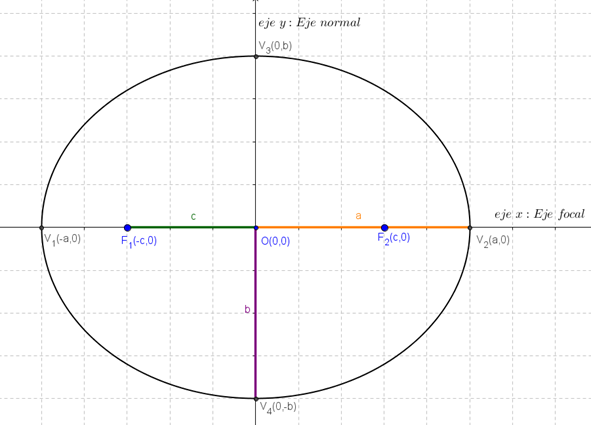
Es la ecuación canónica de la elipse con centro (0,0)(0,0) y eje focal y=0y=0(eje xx).

Busquemos las intersecciones con los ejes:

Si y=0:y=0: x2=a2⇒x=±a⇒V1,2=(±a,0)x2=a2⇒x=±a⇒V1,2=(±a,0)

Si x=0:x=0: y2=b2⇒y=±b⇒V3,4=(0,±b)y2=b2⇒y=±b⇒V3,4=(0,±b)

Estos cuatro puntos se denominan vértices de la elipse.

aa se denomina semieje mayor

bb es el semieje menor

cc es la semidistancia focal: (distancia del centro a un foco)

2c es la distancia entre los focos

Eje focal: es la recta que pasa por los focos, en este caso el eje x

Observen que el centro es centro de simetría de la elipse.

Si en la ecuación canónica anterior permutamos x por y ( x↔↔y) queda:

 y2a2+x2b2=1,a>by2a2+x2b2=1,a>b

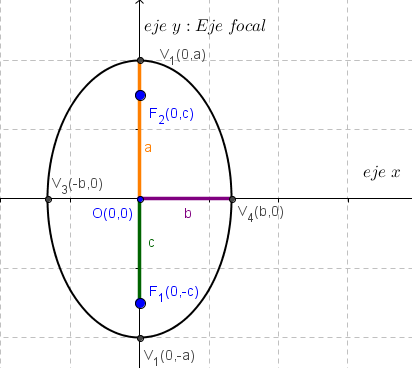
Es la ecuación canónica de la elipse con centro(0,0)(0,0) y eje focal x=0x=0 (eje yy).

$$